Sayılar bir şeyin
niceliği hakkında kesin sonuçlar sunar. Sayılar arasındaki
fark, yani
değişim olmuş veya olacaklar hakkında bazı
fikirler verir. Sayıların
oranları nicelikler üzerinde daha rahat
düşünme imkanı sağlar.
Değişim oranları ise niceliğin trendini (
eğilimini) görmemizi ve ortaya çıkacak
değişimin gücünü idrak etmemizi kolaylaştırır.
Örneğin; Bir bölgenin toplam geliri o bölgenin ne kadar zengin olduğunu gösterir. Anlamlıdır. Bu zenginliğin bölge halkı tarafından nasıl paylaşıldığını bilmek ise farklı bir heyecan uyandırır. Gelir dağılımındaki eşitsizlik durumu bölge hakkında çok çarpıcı bilgiler sunar. Mesela restoranımızın yeni şubesini nerede açmalıyız? sorusunun cevabını bulmak için bu bilgiden faydalanabiliriz. Servet, bölge halkına eşit şekilde mi dağılmış, yoksa bir kaç kişinin elinde mi tutuluyor? Bunu bilmek kesinlikle yeni şubemizin yerini belirlemede etkili olacaktır. İşte bu tarz çarpıcı bilgileri ortaya çıkarabilmek için bir takım sayıların oranlarından faydalanırız.
Bu yazımızda bir dağılımdaki eşitsizliğin derecesini ölçmemizi sağlayan oranlara odaklanıyoruz. İstatistikçiler bu oranları kullanarak bir yığın sayı hakkında çarpıcı çıkarımlar yapabilmektedir.
Bir Dağılımdaki Eşitsizliğin Görünümü
1905 yılında Max Otto Lorenz gelir dağılımının görüntüsünü, iki ekseninde yüzde değerler bulunan bir grafik (dik koordinat sistemi) üzerindeki eğri ile ifade etmiştir. Bu eğriye Lorenz Eğrisi (Lorenz Curve) denir.
Yukarıdaki ekonomi örneği üzerinden gidersek; Dik koordinat sisteminde x eksenine en fakirden en zengine sıralanmış nüfusun kümülatif yüzdelik dilimleri yerleştirilir. İlk %20, ilk %40, ilk %60...%100 gibi. y eksenine ise gelirin kümülatif yüzdelik dilimleri yerleştirilir. Gelirin %20'si, %40'ı....%100'ü gibi.
Sonra nüfusun yüzde kaçı gelirin yüzde kaçına sahip olduğu grafik üzerinde işaretlendiğinde ortaya bir eğri çıkar. Ortaya çıkan bu Lorenz Eğrisi gelir dağılımı hakkında bazı çıkarımlar yapma imkanı verir.
Aşağıdaki kalın gri çizgi ile ayrılmış iki örneği inceleyelim;
Resmi büyütmek için tıklayın (resmi)
Örnekleri incelediğimizde; (0,0) ve (100,100) noktalarının birleşimi olan 45 derecelik turuncu doğrunun mükemmel eşitliği ifade ettiğini görebiliriz. Çünkü doğru boyunca nüfusun %20'si gelirin %20'sine, %40'ı gelirin %40'ına vs. sahip olduğunu söyleyebiliriz. Bu durumda grafiğin (0,0),(100,0), (100,100) noktalarının birleşimi ile oraya çıkan çizginin ise mükemmel eşitsizliği ifade ettiğini söyleyebiliriz. Bu çizgiyi aşağıdaki grafikte kırmızı renk ile ön plana çıkardık.
Bu durumda matematiksel olarak şunu söylemek mümkün. Lorenz Eğrisi mükemmel eşitlik çizgisine yaklaştıkça gelir dağılımı daha eşit hale gelir. Lorenz Eğrisi mükemmel eşitsizlik çizgisine yaklaştıkça da dağılım giderek eşit olmaktan uzaklaşır.
Peki, bizim gelir dağılımımızın ne kadar eşit olduğunu nasıl ifade edebiliriz?
Dağılımdaki Eşitsizliğin Ölçüsü
1912 yılında İtalyan istatistikçi Corrado Gini bir dağılımın eşitsizliğini ölçebilmek için Gini Katsayısını (Gini Coefficient) geliştirdiğini duyurmuştur. Gini katsayısı Lorenz Eğrisinden faydalanır. Bir takım hesaplar sonucunda 0 ile 1 arasında bir sayı çıkar ve bu sayı eşitsizliğin büyüklüğünü ifade eder.
Aslında mantık çok basit; Lorenz Eğrisinin üst kısmında kalan alan mükemmel eşitliğe ne kadar uzak olduğumuzu ifade eder. Bu alan küçüldükçe daha eşit bir dağılım elde ederiz. Tam da bu fikirle yola çıktığımızda bu alanın mükemmel eşitlik altındaki alana oranı bize Gini Katsayısını verir.
G ile gri alanı, S ile sarı alanı ifade edelim. Basitçe şu alan hesabı ile Gini Katsayısını elde edebiliriz;
Lorenz Eğirisi bir eğri olabileceği için alan hesabında integral kullanmak gerekebilir. Eğriyi L(x) diye isimlendirdiğimiz bir fonksiyon ile ifade edersek. Gini katsayısı şu şekilde hesaplanır.
Hataya açık başka pratik yöntemler de mevcut. Onlara burada değinmeyeceğim. Daha sonraki yazılarımızda bir takım senaryolar için hesaplamalar yapacağız. Şimdilik hesap kısmı için bu kadarı ile yetinelim.
Gini Katsayısı ve Lorenz Eğrisi Ne Anlatır Ne Anlatmaz?
Gini katsayısı 0 ile 1 arasında değişen bir sayıdır. Bu katsayı ne kadar zengin olunduğunu ifade etmez. Mevcut zenginliğin nasıl paylaşıldığını ifade eder. Eşitsizlik derecesini ifade eden bu sayı 0'a yaklaştıkça daha eşit bir dağılım görürüz.
İlk resimde de görüldüğü üzere Lorenz Eğrisi mükemmel eşitlik çizgisine sağdaki düşük toplam gelir örneğinde daha yakın. Doğal olarak Gini Katsayısı sağdaki durumda 0'a daha yakın. Tersi de olabilirdi. Sonuç olarak Gini katsayısı toplam gelir hakkında bilgi vermez. Oranlar üzerinden hesaplama yapıldığı için toplam gelir bu katsayıyı etkilemez. Tabi ki sosyolojik olarak toplam gelirin artması dar gelirlilerin kazancını da etkileyebilir. Ancak matematiksel olarak bunu göz ardı ederiz.
Gerçek hayatta da örneğimize benzer sonuçlarla karşılaşmak mümkün. Dünya Gini Katsayılarına baktığımızda 2008 yılında yapılan bir ölçümde Afganistan'ın katsayısı 0,27 görünürken, en yakın 2007 yılında yapılan bir ölçümde Amerika Birleşik Devletlerinin katsayısı 0,45 olduğu tespit edilmiş. Sanırım servet az iken paylaşmak daha kolay oluyor gerçeğinin bir yansıması bu.
Dünya gelir dağılımın ne kadar eşit olduğunu bilmek istersiniz diye düşünüyorum.
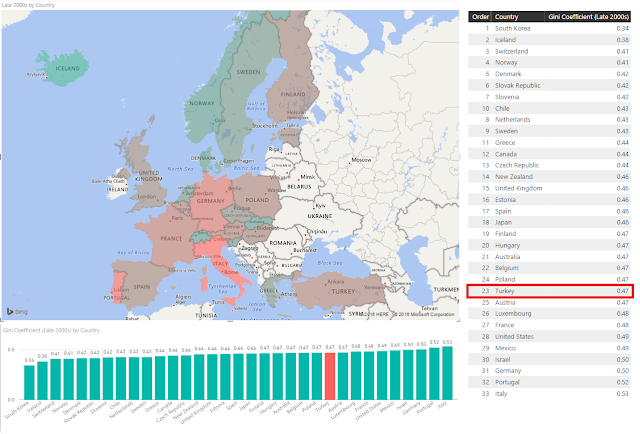
Dünya Gelir Dağılımındaki Eşitsizlik Değerleri (Gini Katsayıları)
İşte 2000'li yılların sonlarına doğru ülkelerin vergilendirmeden önceki Gini katsayıları:
Yukarıdaki raporu Power BI ile yaptım. Ham veriye ve bir takım raporlara şu linkten erişebilirsiniz:
Gini Katsayısı ve Lorenz Eğrisi sadece ekonomide değil, sosyoloji, ekoloji ve mühendislik gibi daha bir çok alanda karşımıza çıkmaktadır. Siz de bu mantıktaki herhangi bir dağılımın eşitsizlik durumunu açığa çıkarmak için Gini Katsayısını ve Lorenz Eğrisini kullanabilirsiniz. Mesela kaynak-iş yükü optimizasyonunu yapabilmek için iş yükünün kaynaklara nasıl dağıtıldığını görmek isteyebilirsiniz.
İstatistik eğlencelidir!
Sonraki yazılarımızda R dilini kullanarak bir dağılımın Lorenz Eğrisinin ve Gini Katsayısının nasıl elde edilebileceğini inceleyeceğiz.